一、因子相关性检验的原因：多重共线性

我们通过单因子测试部分筛选出一批有效因子，但以上因子不能直接入库。因子本身可以根据具体的经济含义进行大类划分，同类型的因子间存在较强的相关性，若不经相关性筛选直接入库，根据不同因子进行多元线性回归求预期收益率时，会出现多重共线性问题。计量经济学中，多重共线性是指回归模型中的一些或全部解释变量存在“完全”或准确的线性关系（各变量间高度相关）。

因此，有效因子筛选出后，首先需要根据大类对因子的相关性进行T检验，对于相关性较高的因子，要么舍弃显著性较低的因子，要么进行因子合成。

多重共线性的数学解释如下：

Y=β₁+β₂X₂ᵢ+β₃X₃ᵢ+…+βₖXₖᵢ+μᵢ,i=1,2,…,n

会存在两种情况：

1.C₂X₂ᵢ+C₃X₃ᵢ+…+CₖXₖᵢ=常数向量，Cᵢ不全为0→Xᵢ 间存在完全共线

2.C₂X₂ᵢ+C₃X₃ᵢ+…+CₖXₖᵢ+Vᵢ=常数向量，Cᵢ不全为0，Vᵢ为随机误差项，→Xᵢ间存在完全共线

多重共线性导致的后果：

1.完全共线性下参数估计量不存在

2.近似共线性下OLS估计量非有效

我们首先定义方差膨胀因子（variance- inflating factor, VIF）为 VIF=1/(1−rᵢⱼ) ，指参数估计量的方差由于出现多重共线性而膨胀，随着相关系数增加，VIF显著增加。

以二元线性模型为例：Y=β₁+β₂X₂ᵢ+β₃X₃ᵢ+μᵢ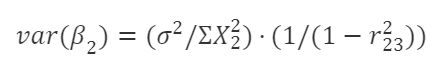

相关系数的平方和

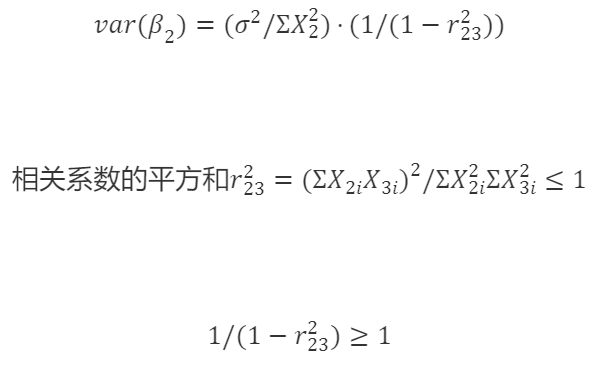
• 完全不共线（完全不相关）：

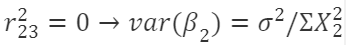
• 近似共线：

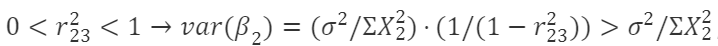
，越接近1，方差↑

• 完全共线：

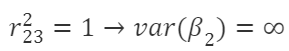
，方差无限大

3.参数估计量经济含义不合理

4.变量的显著性检验（t检验）失去意义

5.模型的预测功能失效：通过多元线性模型拟合出的预测收益率极其不准确，模型失效。

二、步骤一：同类型因子的相关性检验

检验新求出的因子与已入库因子的相关性。通常来说，有两类数据求相关性：

1.根据所有token在回测期间的因子值求相关

2.根据所有token在回测期间的因子超额收益值求相关

超额收益=多头组收益−基准收益，收益=ln(closeₜ/close₋₁)

我们所求的每个因子对token的收益率都有一定的贡献和解释能力。进行相关性检验**，是为了找到对策略收益有不同解释和贡献的因子，策略的最终目的是收益**。如果两个因子对收益的刻画是相同的，即使两个因子值存在很大差别也无意义。因此，我们并不是想找到因子值本身差异大的因子，而是想找到因子对收益刻画不同的因子，所以最终选择了用因子超额收益值求相关。

我们的策略是日频，所以按回测区间的日期计算因子超额收益之间的相关系数矩阵

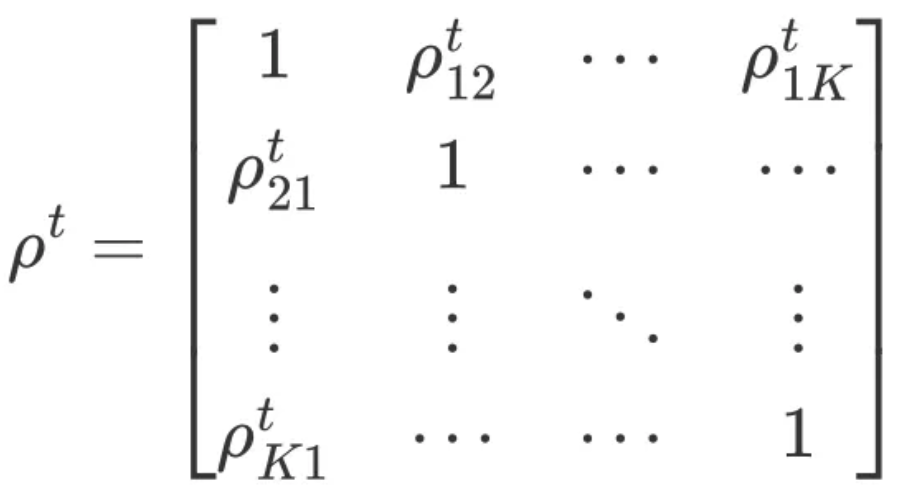
编程求解与库内相关最高的前n个因子：

def get_n_max_corr(self, factors, n=1):

factors_excess = self.get_excess_returns(factors)

save_factor_excess = self.get_excess_return(self.factor_value, self.start_date, self.end_date)

        if len(factors_excess) < 1:

return factor_excess, 1.0, None factors_excess[self.factor_name] = factor_excess['excess_return']

factors_excess = pd.concat(factors_excess, axis=1)

factors_excess.columns = factors_excess.columns.levels[0] # get corr matrix

factor_corr = factors_excess.corr()

factor_corr_df = factor_corr.abs().loc[self.factor_name]

max_corr_score = factor_corr_df.sort_values(ascending=False).iloc[1:].head(n)

return save_factor_excess, factor_corr_df, max_corr_score

三、步骤二：因子取舍、因子合成

对于相关性较高的因子集合，可以采取两种方式处理：

（1）因子取舍

根据因子本身的ICIR值、收益率、换手率、Sharpe 比率，挑选某维度下最有效的因子进行保留，删除其他因子。

（2）因子合成

对因子集合中的因子进行合成，截面上尽可能多的保留有效信息

F=w₁∗f₁+w₂∗f₂+…+wₙ∗fₙ，F为最终的合成因子，f为需要进行合成的因子

假设当前有3个待处理的因子矩阵：

synthesis = pd.concat([a,b,c],axis = 1) 

synthesis

a b c

BTC.BN 0.184865 -0.013253 -0.001557

ETH.BN 0.185691 0.022708 0.031793

BNB.BN 0.242072 -0.180952 -0.067430

LTC.BN 0.275923 -0.125712 -0.049596

AAVE.BN 0.204443 -0.000819 -0.006550

... ... ... ...

SOC.BN 0.231638 -0.095946 -0.049495

AVAX.BN 0.204714 -0.079707 -0.041806

DAO.BN 0.194990 0.022095 -0.011764

ETC.BN 0.184236 -0.021909 -0.013325

TRX.BN 0.175118 -0.055077 -0.039513

2.1 等权加权

各因子权重相等（w=1/因子个数），综合因子=各因子值加总求平均。

Eg.动量类因子，一个月收益率、两个月收益率、三个月收益率、六个月收益率、十二个月收益率，这六个因子的因子载荷各占1/6的权重，合成新的动量因子载荷，然后再重新进行标准化处理。

synthesis1 = synthesis.mean(axis=1) # 按行求均值

2.2 历史IC加权、历史ICIR、历史收益加权

用回测期的IC值（ICIR值、历史收益值）对因子进行加权。过去有很多期，每一期都有一个IC值，所以用它们的均值作为因子的权重。通常使用回测期IC的均值（算数平均值）作为权重。

# 权重归一化（后文中的因子加权方式也基本都需要进行权重归一化）

w_IC = ic.mean() / ic.mean().sum()

w_ICIR = icir.mean() / icir.mean().sum()

w_Ret = Return.mean() / Return.mean().sum()

synthesis2 = (synthesis * w_IC).sum(axis=1)

synthesis2 = (synthesis * w_ICIR).sum(axis=1)

synthesis2 = (synthesis * w_Ret).sum(axis=1)

2.3历史IC半衰加权、历史ICIR半衰加权

2.1与2.2都是计算算数平均值，回测期的每一次IC、ICIR对于因子的作用被默认为相同。

但现实中，回测期的每一期对于当期的影响程度不完全相同，存在时间上的衰减。越接近当前期的时期，影响越大，越远影响越小。在此原理，求IC权重前首先定义一个半衰权重，距离当期越近的权重值越大、越远权重越小。

半衰权重数学推导：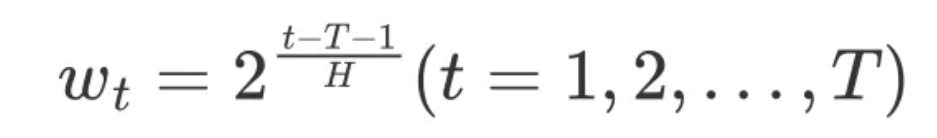

* 半衰期H：每向前推H期，权重值以指数下降的方式降低一半* T：考虑回测的期数

# 半衰权重

def Decay(H,T):

t = np.arange(T+1)[1:]

wt = 2**((t-T-1)/H) #半衰权重

decay = wt/wt.sum() #归一化

return decay

# 历史IC半衰加权

w_bs = Decay(6,12) # 假设T=12，H=6

ic_bs = ic.mul(w_bs,axis=0)

w = ic_bs.mean()/ic.mean().sum()

synthesis3 = (synthesis * w).sum(axis=1)

# 历史ICIR半衰加权

# 历史ICIR半衰加权在历史IC半衰加权的基础上，除以IC值的标准差。

w_bs = bs(6,12)

ic_bs = ic.mul(w_bs,axis=0)

ir_bs = ic_bs.mean()/ic.std()

w = ir_bs.mean()/ir_bs.mean().sum()

synthesis3 = (synthesis * w).sum(axis=1)

2.4 最大化ICIR加权

通过求解方程，计算最优因子权重w使得ICIR最大化

协方差矩阵的估计问题：协方差矩阵用于衡量不同资产之间的关联性。统计学中常以样本协方差矩阵代替总体协方差矩阵，但在样本量不足时，样本协方差矩阵与总体协方差矩阵的差异会很大。所以有人提出了压缩估计的方法，原理是使估计协方差矩阵与实际协方差矩阵之间的均方误差最小

方式：

1.样本协方差矩阵

# 最大化ICIR加权(样本协方差)

ic_cov = np.array(ic.cov())

inv_ic_cov = np.linalg.inv(ic_cov)

ic_vector = np.mat(ic.mean())

w = inv_ic_cov * ic_vector.T

w = w / w.sum()

synthesis4 = (synthesis * pd.DataFrame(w,index=synthesis.columns)[0]).sum(axis=1)

2.Ledoit-Wolf收缩：引入一个缩小系数，将原始的协方差矩阵与单位矩阵进行混合，以减少噪音的影响。

# 最大化ICIR加权(Ledoit-Wolf压缩估计协方差)

from sklearn.covariance import LedoitWolf

model=LedoitWolf()

model.fit(ic)

ic_cov_lw = model.covariance_

inv_ic_cov = np.linalg.inv(ic_cov_lw)

ic_vector = np.mat(ic.mean())

w = inv_ic_cov*ic_vector.T

w = w/w.sum()

synthesis4 = (synthesis * pd.DataFrame(w,index=synthesis.columns)[0]).sum(axis=1)

3.Oracle近似收缩：对Ledoit-Wolf收缩的改进，目标是通过对协方差矩阵进行调整，从而在样本大小较小的情况下更准确地估计真实的协方差矩阵。（编程实现与Ledoit-Wolf收缩同理）

2.5 主成分分析PCA

主成分分析（Principal Component Analysis，PCA）是一种用于降维和提取数据主要特征的统计方法。其目标是通过线性变换，将原始数据映射到一个新的坐标系，使得数据在新坐标系下的方差最大化。

具体而言，PCA首先找到数据中的主成分，也就是数据中方差最大的方向。然后，它找到与第一个主成分正交（无关）且具有最大方差的第二个主成分。这个过程一直重复，直到找到数据中所有的主成分。

# 主成分分析(PCA)

from sklearn.decomposition import PCA

model1 = PCA(n_components=1)

model1.fit(f)

w=model1.components_

w=w/w.sum()

weighted_factor=(f*pd.DataFrame(w,columns=f.columns).iloc[0]).sum(axis=1)